Funktionen
Polynom-, Wurzel- oder Logarithmusfunktion – mathematische Funktionen gibt es viele. Zur Abiturprüfung in Mathematik solltest du alle draufhaben. Nutze die folgenden Beispielaufgaben für die Vorbereitung auf das Abitur.
Funktionen – Aufgaben
Aufgabe 1
Gegeben sei die Gerade g durch ihre Funktionsgleichung y = g (x) und ein Punkt P1 (x1 | y1). Beschreiben Sie ein Verfahren, mit dem Sie entscheiden können, ob P1 auf der Geraden g liegt.
Aufgabe 2
Bei einer Elektrizitätsrechnung setzt sich der Preis aus einem Sockelbetrag und einem Anteil, der sich linear mit der verbrauchten Energiemenge in kWh ändert, zusammen. Ein Werk bietet folgende Tarife an:
A: 1000 kWh kosten 107,00 €, 500 kWh kosten 57,00 €,
B: 7 kWh kosten 2,45 € und jede weitere kWh kostet 0,35 €,
C: Bei einem Sockelbetrag von 12,00 € kostet jede kWh 0,07 €.
Bestimmen Sie zu jedem der drei Tarife eine Funktionsgleichung, die den Preis als Funktion der verbrauchten Energie beschreibt.
Funktionen - Lösungen
Aufgabe 1
Sie setzen in die Funktionsgleichung y = g (x) die Koordinaten des Punktes P1 (x1 | y1) ein.
Ist die entstehende Aussage y1 = g (x1) wahr, dann liegt der Punkt auf der Geraden.
Aufgabe 2
Sie beschreiben den Preis durch y und die verbrauchte Energie durch x.
Die Punkte lauten:
P1 (500 | 57) und P2 (1000 | 107).
Sie berechnen zunächst m:

Mitternachtsformel
Komplizierte Gleichungen lösen? Die Mitternachtsformel – oft auch ABC-Formel oder p-q-Formel genannt – macht es möglich. Zur Mathe-Prüfung beim Abitur oder Matura solltest du sie also können. Teste dein Wissen jetzt mit den folgenden Aufgaben.
Aufgaben
Berechnen Sie die Lösungsmengen der Gleichungen.
a) 3x² – 6x + 15 = 0
b) – 0,25x² + 1,5x – 2 = 0
c) – 4x² + 12x – 9 = 0
Lösungen
Sie dividieren zunächst durch den Koeffizienten vor x² und wenden danach die p-q-Formel auf die entstehende quadratische Gleichung an.

Lineare Gleichungssysteme
Ob Gleichsetzungs-, Einsetzungs- oder Additionsverfahren – mit linearen Gleichungssystemen hast du ganz schön zu rechnen. Kommst du dabei immer auf die richtige Lösung? Nutze unsere Übungsaufgaben zum Lernen und du weißt, ob du fit fürs Abitur bist.
Aufgaben
Aufgabe 1
Bestimmen Sie den Schnittpunkt zweier Geraden mit den Gleichungen
g1: y = 2x + 3 und g2: y = 3x – 4 .
Beschreiben Sie Ihre Rechenschritte kurz.
Aufgabe 2
Beschreiben Sie die drei verschiedenen Arten von Lösungsmengen, die ein LGS haben kann.
Aufgabe 3

Lösungen
Aufgabe 1

Aufgabe 2
Die Lösungsmenge eines LGS enthält entweder eine eindeutige Lösung, unendlich viele Lösungen oder sie ist leer, wenn es keine Lösung gibt.
Aufgabe 3

Matrizenrechnung
Lineare Zusammenhänge einfach und schnell miteinander vergleichen oder mit diesen rechnen – die Matrizenrechnung vereinfacht es. Bist du darin auf deine Abiturprüfung in Mathematik vorbereitet? Die Übungsaufgaben geben dir Gewissheit.
Aufgaben
Aufgabe 1
Stellen Sie das folgende LGS in Matrizenschreibweise dar und lösen Sie es danach mithilfe der erweiterten Koeffizientenmatrix.
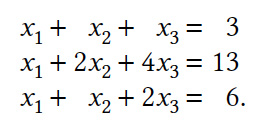
Aufgabe 2
Führen Sie die folgenden Matrix-Vektor-Multiplikationen aus, sofern sie möglich sind.
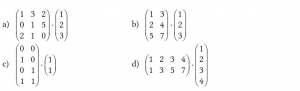
Lösungen
Aufgabe 1

Aufgabe 2
Eine Multiplikation ist bei b nicht möglich, da die Matrix nur zwei Spalten hat.

Vektoren und Vektorgeometrie
Egal, ob du im Grund- oder Leistungskurs Mathematik bist: Zur Abiturprüfung solltest du die Matrizenrechnung beherrschen. Überprüfe dein Können jetzt mit unseren Übungsaufgaben auf Abiturniveau.
Aufgaben
Aufgabe 1
Beschreiben Sie die Addition von Vektoren.
Aufgabe 2

Lösungen
Aufgabe 1
Sie addieren jeweils die einzelnen Komponenten.
Aufgabe 2

![]()
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen